2.1 Introduction :
Depuis quelques dizaines d'années, la diffraction des rayons X a été appliquée à l'étude des structures de surface et des couches superficielles grâce à l'utilisation d'une configuration en incidence rasante qui permet de réduire considérablement la profondeur de pénétration du rayonnement dans les matériaux.
2.2 Principe :
On a longtemps pensé que les rayons
X se propageaient rigoureusement en ligne droite depuis les tentatives
infructueuses de déviation opérées par Röntgen,
"l'inventeur" de ces rayons, ce qui poussait à conclure
que, du point de vue des rayons X, tous les milieux, quels qu'ils soient,
avaient un indice égal à 1.
En réalité, cet indice ne vaut pas l'unité mais en
diffère de quelques millionièmes ce qui suffit pour justifier
une déviation des rayons.
Il est de la forme :
avec:
d
de l'ordre de
b
de l'ordre de 10-6
Il existe donc un angle d'incidence critique 
c
au-dessus duquel il y a réflexion totale du rayonnement.
L'angle d'incidence pouvant
être défini par :
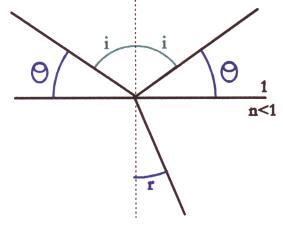
Fig.1
La relation de Descartes nous donne :
)
car on voit +
i = p/2n1 = 1 ( air )
n2 = n ( matériau )
Donc, à l'angle critique : sin(ic) = n
et à ic
correspond c
comme défini ci-dessus d'où :
cos(c)
= n
On est en présence de faibles angles donc :
Cos(c)
# 1 - c
.c/2
# 1 - d
Finalement :
b négligeable,
très
faible.
Cette caractéristique est donc intéressante
en incidence rasante, tous les matériaux se comportant comme des
miroirs pour les rayons X pour des valeurs de <
c
.
Dans ce cas, l'onde transmise devient évanescente.
on peut alors introduire une longueur de pénétration t
de la forme :
Correspondant à une atténuation 1/e.
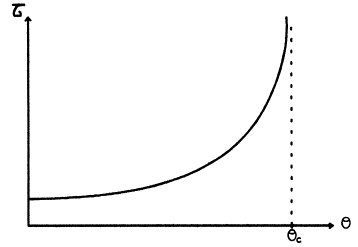
Fig.2
On voit que t est d'autant plus petit que l'angle d'incidence est faible et qu'il augmente fortement au voisinage de
c. <
c
: t = quelques Å >
c
: t = quelques µm
La diffraction, découverte en 1912, est à l'origine
de la cristallographie par rayons X. Un cristal est exposé à
un faisceau de rayon X : on suppose que les atomes agissent comme des
centres d'ondes concentriques diffusant une fraction du rayonnement. On
obtient des rayons diffractés lorsque les rayons réfléchis
par les premiers plans parallèles d'atomes interfèrent de
façon additive selon la loi de Bragg :
2.d.sin()
= n.l
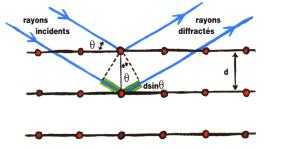
Fig.3
avec :
l
: longueur d'onde
:
angle d'incidence
d
: distance entre 2 plans d'atomes
On ne vérifie la loi de Bragg que pour des valeurs de l
< 2d, c'est à dire avec des
rayons X.
2.4 Principe des mesures :
Expérimentalement, on mesure l'intensité réfléchie par la surface du matériau étudié en fonction de l'angle d'incidence ce qui nous donne la réflectivité.
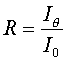
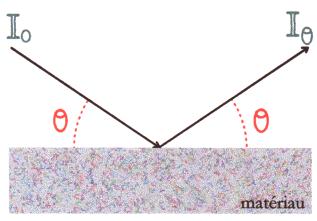
Fig.4
Cette réflectivité donne des renseignements sur la structure
du matériau perpendiculairement à la surface au point de
réflexion (variation de densité, composition…).
Les indices étant très proches de 1,
les angles d'incidence utilisables sont très faibles. En effet
on observe une forte diminution de la réflectivité quand
l'angle d'incidence augmente (supérieur à l'angle critique).
Par exemple, pour des rayons X de longueur d'onde l#
1.54 Å,
On obtient :
c
= 2.7.10-3 rad pour l'eau
c
= 10.10-3 rad pour l'or
En pratique, on travaille sur des angles allant de 1 à 70.10-3
radians.
Cette propriété permet donc d'effectuer une analyse en épaisseur, non destructive, de certaines caractéristiques superficielles d'un échantillon avec une résolution proche de 50 Å dans les 1000 à 2000 premiers Å.
L'incidence rasante permet également des études structurales des surfaces à l'aide d'un rayonnement synchrotron focalisé ; on peut alors obtenir avec une grande précision des signaux provenant de 1 à 2 couches atomiques seulement.
Ces études sont intéressantes du fait que les surfaces des matériaux présentent le plus souvent un arrangement atomique différent de celui du volume : maille différente surface/volume. L'utilisation du rayonnement synchrotron permet d'identifier les espèces atomiques, de mesurer des distances parallèles et perpendiculaires à la surface donc de donner les différentes mailles présentes dans le matériau et d'étudier les relations entre couche externe et substrat.
Remarque :
Ces études nécessitent des mises en œuvre complexes
: temps de collecte des résultats long, "pureté"
du milieu autour du matériau. (cf. § 4.)
2.5 Utilisation de la réflectivité :
Théoriquement, en un point donné, la réflectivité (fonction de l'angle d'incidence
et
de l'indice n du matériau) décroît régulièrement
avec l'augmentation de l'angle ,
or en pratique, on observe une diminution beaucoup plus rapide de R pour,
par exemple, une lame de silicium polie.
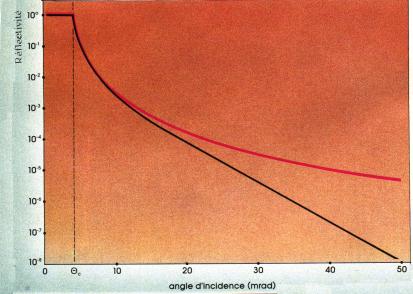
Fig.5
Ceci est dû aux imperfections de la surface du silicium. On introduit donc un paramètre de rugosité (qui explique la courbe expérimentale ) déterminé très précisément à 0.1 Å prés.
Il est utilisé lors de l'étude de matériaux à surface reconstruite qui peuvent être schématisés comme suit (dans le cas d'un multicouches vu plus loin) :
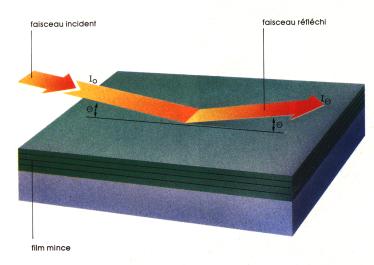
Fig.6
Ici R ne décroît plus régulièrement mais présente des ondulations dues aux interférences provoquées par les réflexions multiples sur les surfaces : On obtient des franges dites de Kiessig (physicien allemand, leur "inventeur" en 1930 ) qui permettent de déterminer très précisément l'épaisseur des films en étudiant les écarts entre les pics de la courbe de variation de la réflectivité.
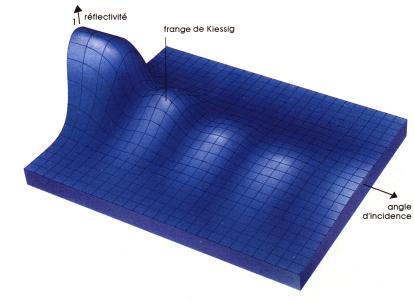
Fig.7
Evidemment, si on augmente le nombre de films (comme dans le cas des traitements multicouches du verre par exemple cf. Fig.6), on assiste à une multiplication des interférences qui donnent naissance à de nouvelles franges appelées pics de Bragg qui permettent d'avoir accès aux caractéristiques de chaque couche (épaisseur, rugosité aux interfaces, densité…) au moyen d'outils mathématiques puissants d'autant plus nécessaires dans le cas d'absence de données initiales (aucun renseignement ni sur la nature ni sur la densité des couches.
